배열의 크기 조정 - realloc 함수
- 일정한 크기의 배열이 주어졌을 때, 그 크기를 키우려면 어떻게 해야 할까?
- 단순하게 현재 배열이 저장되어 있는 메모리 위치의 바로 옆에 일정 크기의 메모리를 더 덧붙이면 되겠지만, 실제로는 다른 데이터가 저장되어 있을 확률이 높다.
- 따라서 안전하게 새로운 공간에 큰 크기의 메모리를 다시 할당하고 기존 배열의 값들을 하나씩 옮겨줘야 한다.
- 따라서 이런 작업은 O(n), 즉 배열의 크기 n만큼의 실행 시간이 소요될 것

연결 리스트: 도입
- 데이터 구조는 우리가 컴퓨터 메모리를 더 효율적으로 관리하기 위해 새로 정의하는 구조체 (일종의 메모리 레이아웃, 또는 지도)
- 배열에서는 각 인덱스의 값이 메모리상에서 연이어 저장되어 있다.
- 하지만 꼭 그럴 필요가 있을까? 각 값이 메모리상의 여러 군데 나뉘어져 있다고 하더라도 바로 다음 값의 메모리 주소만 기억하고 있다면 여전히 값을 연이어서 읽어들일 수 있다. 이를 ‘연결 리스트’라고 한다

- 그림과 같이 크기가 3인 연결 리스트는 각 인덱스의 메모리 주소에서 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장한다.
- 연결 리스트의 가장 첫 번째 값인 1은 2의 메모리 주소를, 2는 3의 메모리 주소를 함께 저장
- 3은 다음 값이 없기 때문에 NULL (\0, 즉 0으로 채워진 값을 의미합니다)을 다음 값의 주소로 저장
연결 리스트는 아래 코드와 같이 간단한 구조체로 정의할 수 있다.

- node 라는 이름의 구조체는 number 와 *next 두 개의 필드가 함께 정의되어 있다.
- number는 각 node가 가지는 값, *next 는 다음 node를 가리키는 포인터
- 여기서 typedef struct 대신에 typedef struct node 라고 ‘node’를 함께 명시해 주는 것은, 구조체 안에서 node를 사용하기 위함
연결 리스트: 코딩
앞서 정의한 구조체를 활용해서 실제로 연결 리스트를 구현해보기



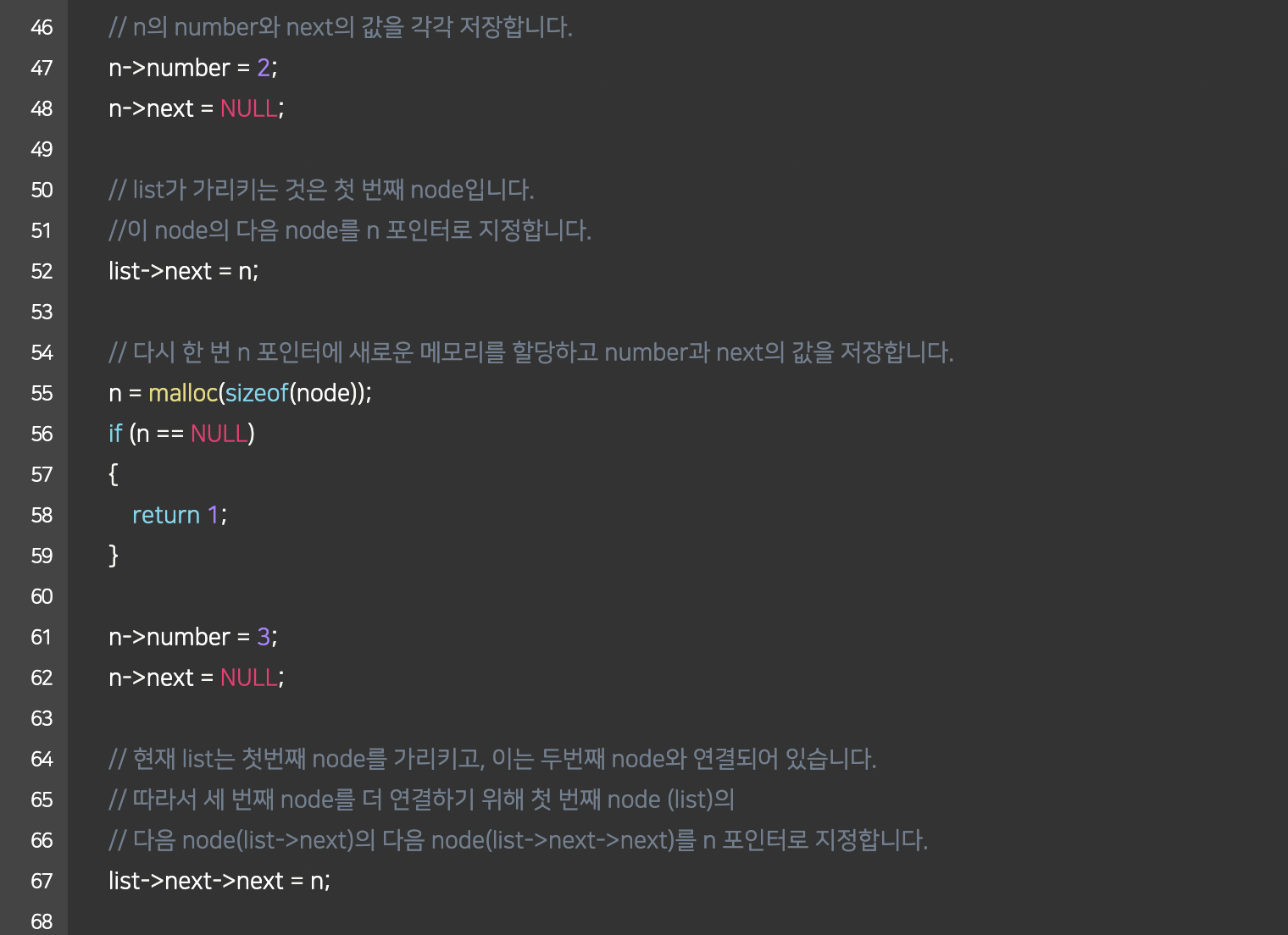

연결 리스트: 시연
- 배열과 비교해서 연결 리스트는 새로운 값을 추가할 때 다시 메모리를 할당하지 않아도 된다는 장점이 있다.
- 하지만 이런 유동적인 구조는 그 대가가 따릅니다. 구조가 정적인 배열과 달리 연결 리스트에서는 임의 접근이 불가능
- 연결 리스트에 값을 추가하거나 검색하는 경우를 생각해 보면,
- 이를 위해서는 해당하는 위치까지 연결 리스트의 각 node들을 따라 이동해야 한다.
- 따라서 연결 리스트의 크기가 n 일때 그 실행 시간은 O(n)이 된다.
- 배열의 경우 임의 접근이 가능하기 때문에 (정렬 되어 있는 경우) 이진 검색을 이용하면 O(log n)의 실행 시간이 소요 되는 것에 비해서 다소 불리한 것
- 이처럼 여러 데이터 구조는 각각 장단점이 존재한다.
- 프로그래밍을 할 때 목적에 부합하는 가장 효율적인 데이터 구조를 고민해서 사용하는 것이 중요!
연결 리스트: 트리
- 트리는 연결리스트를 기반으로 한 새로운 데이터 구조
- 연결리스트에서의 각 노드 (연결 리스트 내의 한 요소를 지칭)들의 연결이 1차원적으로 구성되어 있다면, 트리에서의 노드들의 연결은 2차원적으로 구성되어 있다
- 각 노드는 일정한 층에 속하고, 다음 층의 노드들을 가리키는 포인터를 가지게 된다.
- 가장 높은 층에서 트리가 시작되는 노드를 ‘루트’라고 한다. 루트 노드는 다음 층의 노드들을 가리키고 있고, 이를 ‘자식 노드’라고 한다.
※ 아래 그림은 트리의 예시. 나무가 거꾸로 뒤집혀 있는 형태를 생각하면 된다.
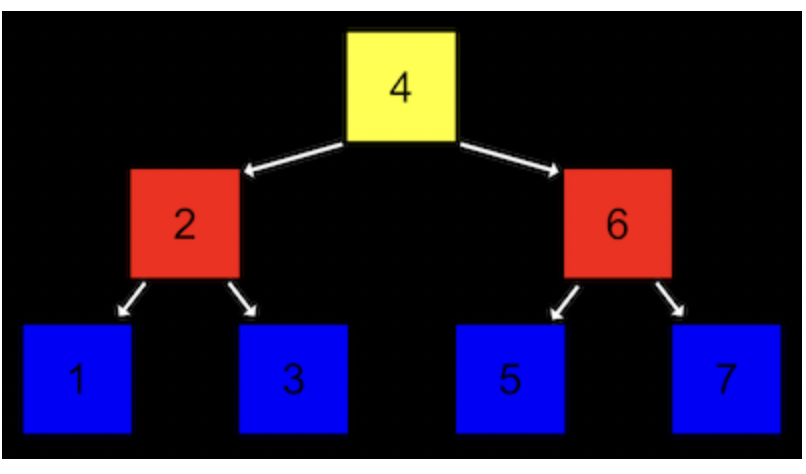
- 위 그림에 묘사된 트리는 구체적으로 ‘이진 검색 트리’
- 각 노드가 구성되어 있는 구조를 살펴보면 일정한 규칙을 알 수 있다.
- 먼저 하나의 노드는 두 개의 자식 노드를 가진다.
- 또 왼쪽 자식 노드는 자신의 값 보다 작고, 오른쪽 자식 노드는 자신의 값보다 크다.
- 따라서 이런 트리 구조는 이진 검색을 수행하는데 유리
아래 코드에서는 이진 검색 트리의 노드 구조체와 “50”을 재귀적으로 검색하는 이진 검색 함수를 구현하였다. (차근히 읽어보기)
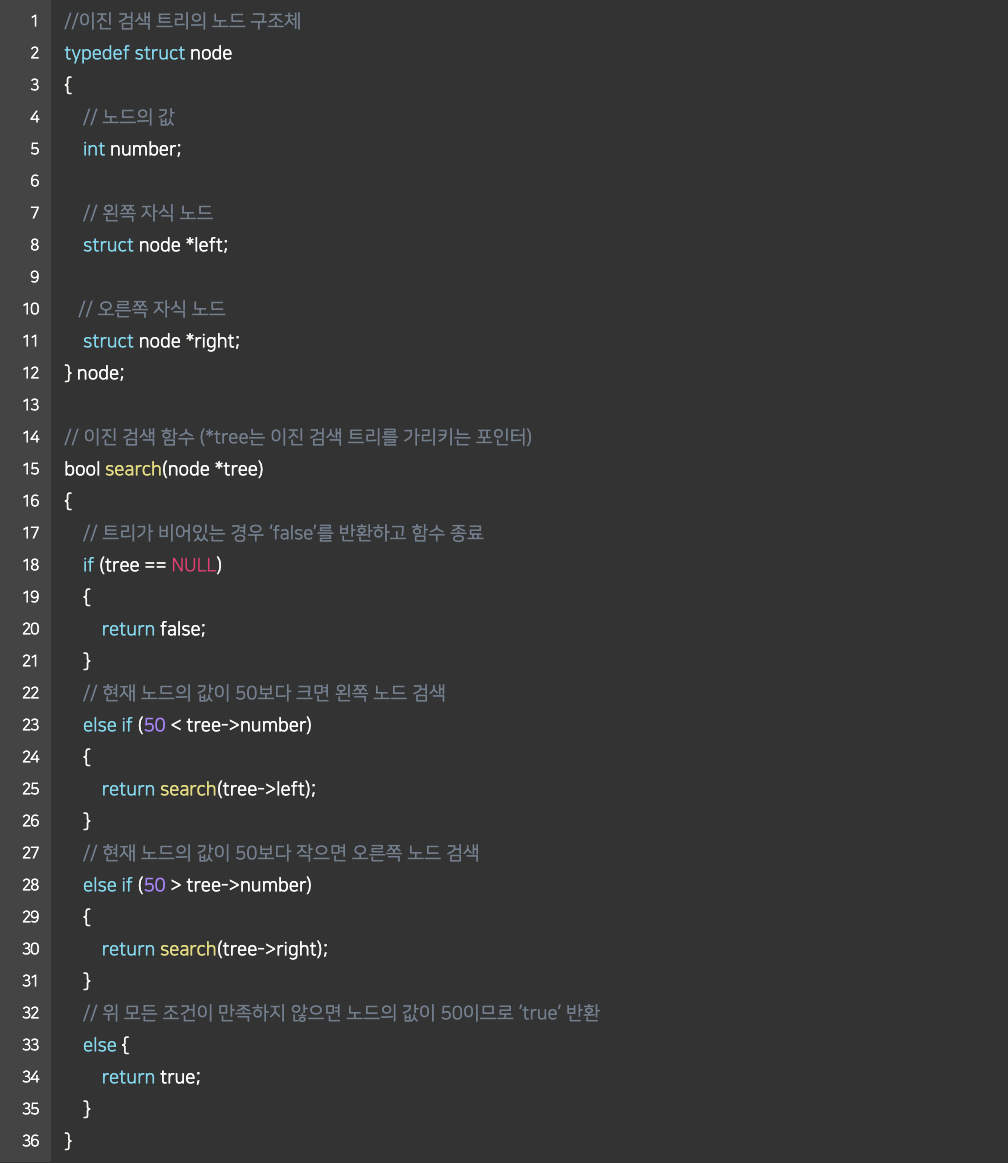
이진 검색 트리를 활용하였을 때 검색 실행 시간과 노드 삽입 시간은 모두 O(log n)
'boostcourse > CS50' 카테고리의 다른 글
| CS50 6. 자료구조(2) - 해시 테이블, 트라이, 큐/스택/딕셔너리 (0) | 2022.10.25 |
|---|---|
| CS50 5. 메모리(4) - 파일 쓰기, 파일 읽기 (0) | 2022.10.25 |
| CS50 5. 메모리(3) - 메모리 할당과 해제/ 메모리 교환, 스택, 힙 (0) | 2022.10.25 |
| CS50 5. 메모리(2) - 문자열, 문자열 비교, 문자열 복사 (0) | 2022.10.24 |
| CS50 5. 메모리(1) - 메모리 주소, 포인터 (0) | 2022.10.24 |
