메모리 주소

① 16진수 

• 컴퓨터과학에서는 데이터를 처리하기 위해 숫자를 10진수나 2진수 대신 16진수(Hexadecimal)로 표현하는 경우가 많다.
• 16진수를 사용하면 10진수보다 2진수를 간단하게 나타낼 수 있는 장점이 있기 때문

② 10진수를 16진수로 바꾸어보기

JPG 이미지 파일은 항상 255 216 255 로 시작되고 이것은 10진수다. 하지만 실제 컴퓨터 내에서는 10진수를 사용하지 않는다. 컴퓨터는 0과 1만을 이해할 수 있기 때문.

 

• 먼저 255 216 255를 2진수로 나타내보면 <그림 1>과 같다.
• 2진수로 모든 데이터를 표현하기에는 너무 길어지기 때문에 16진수로 바꾸어 보면,
• 2^4(2의 4제곱)이 16이기 때문에 4bits씩 두 덩어리로 나누어 보면 0000 부터 1111까지는 16진수로 표현할 수 있다.
• 그렇다면 16진수에서 10부터 15까지는 어떻게 표기할까? 10은 a, 11은 b, …, 15는 f를 대입하여 사용
• 4bits씩 16진수로 변환 후 0x를 붙혀 뒤에 오는 문자들이 16진수임을 알려준다.

 

③ 16진수의 유용성

 

• ASCII 코드에 의해 “A, B, C”는 10진수로 65, 66, 67에 해당
• 컴퓨터는 10진수를 이해할 수 없으므로 2진수로 표현해보면  "01000001 01000010 01000011＂이 된다.
• 하지만 16진수로 표현하면 2진수로 표현했을 때 보다 훨씬 간단해 진다.
• 컴퓨터는 8개의 비트가 모인 바이트 단위로 정보를 표현는데,
• 2개의 16진수는 1byte의 2진수로 변환되기 때문에 정보를 표현하기 매우 유용

 

 

⑤ 메모리 주소

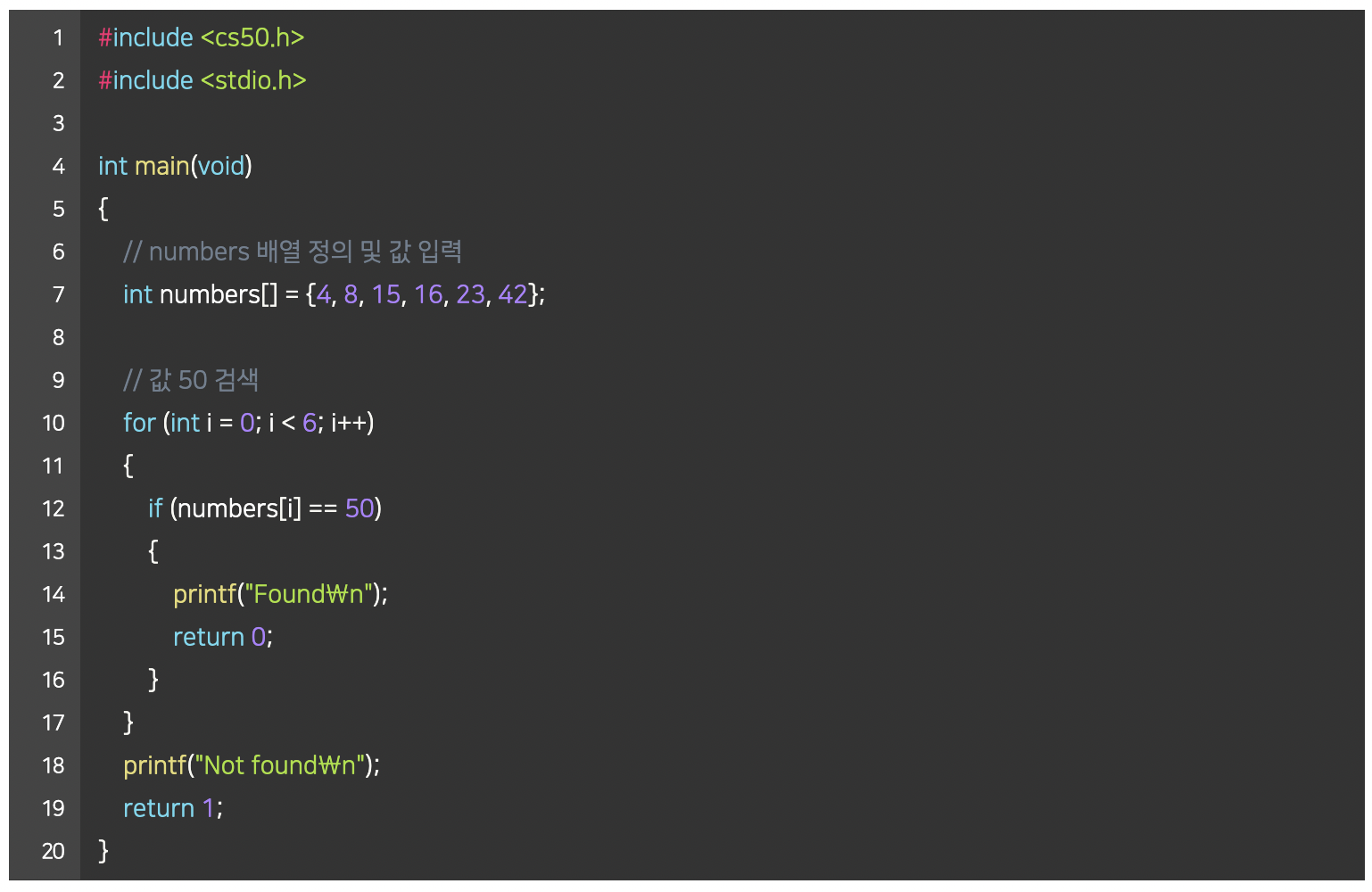
• 정수형 변수 n에 50이라는 값을 저장하고 출력한다고 생각해 보자.
• n 이라는 값은 int 타입이므로, 우리 컴퓨터의 메모리 어딘가에 4바이트 만큼의 자리를 차지하며 저장되어 있을 것 
• C에서는 변수의 메모리상 주소를 받기 위해 ‘&’이라는 연산자를 사용할 수 있다.

• 예를 들어, 위와 같은 코드를 실행하면 ‘0x7ffe00b3adbc’와 같은 값을 얻을 수 있고, 이는 변수 n의  16진법으로 표현된 메모리의 주소이다.
• 반대로 ‘*’를 사용하면 그 메모리 주소에 있는 실제 값을 얻을 수 있다.

• 위 코드는 먼저 n의 주소를 얻고, 또 다시 그 주소에 해당하는 값을 얻어와 출력한 것이므로 결국 ‘50’이라는 값이 출력된다.

포인터

• 지난 강의에서 배웠던 ‘*’ 연산자는 어떤 메모리 주소에 있는 값을 받아오게 해준다.
• 이 연산자를 이용해서 포인터 역할을 하는 변수를 선언할 수도 있다.

• 위 코드를 보면 정수형 변수 n에는 50이라는 값이 저장되어 있다.
• 그리고 *p라는 포인터 변수에 &n 이라는 값, 즉 변수 n의 주소를 저장한다.
• int *p 에서 p앞의 *는 이 변수가 포인터라는 의미이고, int 는 이 포인터가 int 타입의 변수를 가리킨다는 의미
• 따라서 첫 번째 printf문과 같이 포인터 p의 값, 즉 변수 n의 주소를 출력하거나, 두 번째 printft문과 같이 포인터 p가 가리키는 변수의 값, 즉 변수 n의 값을 출력할 수도 있다.

실제 컴퓨터 메모리에서 변수 p는 아래와 같이 저장될 수 있다.

하지만 아래 그림과 같이 실제로 p의 값, 즉 n의 주소값을 생각하지 않고, 추상적으로 단지 p가 n을 가리키고 있다는 것만 생각해도 된다.

실행시간의 상한

• O(n^2): 선택 정렬, 버블 정렬
• O(n log n) 병합 정렬
• O(n): 선형 검색
• O(log n): 이진 검색
• O(1)

실행시간의 하한

• Ω(n^2): 선택 정렬, 버블 정렬
• Ω(n log n) 병합 정렬
• Ω(n) 버블 정렬
• Ω(log n)
• Ω(1): 선형 검색, 이진 검색

버블 정렬을 좀 더 잘 할 수 있는 방법

만약 정렬이 모두 되어 있는 숫자 리스트가 주어진다면?

원래 의사 코드는 아래와 같다.

여기서 안쪽 루프에서 만약 교환이 하나도 일어나지 않는다면 이미 정렬이 잘 되어 있는 상황일 것

따라서 바깥쪽 루프를 ‘교환이 일어나지 않을때’까지만 수행하도록 다음과 같이 바꿀 수 있다.

따라서 최종적으로 버블 정렬의 하한은 Ω(n)이 된다. 상황에 따라서는 선택 정렬보다 더 빠른 방법이 되는 것

재귀

• 함수가 본인 스스로를 호출해서 사용할 수 있는지? 이에 대한 대답은 할 수 있다 이며, 이러한 것을 재귀(Recursion)라고 부른다.

아래와 같이 피라미드 모양을 출력하기 위해 다음과 같은 코드를 작성할 수 있다.

#

##

###

####

• 높이를 입력 받아 중첩 루프를 통해 피라미드를 출력해주는 draw 함수를 정의
• 여기서 꼭 중첩 루프를 써야만 할까? 사실 바깥 쪽 루프는 안 쪽 루프에서 수행하는 내용을 반복하도록 하는 것일 뿐
• 따라서 바깥 쪽 루프를 없앤 draw함수를 만들고, 이를 ‘재귀적으로’ 호출하도록 해서 똑같은 작업을 수행할 수 있다.
• 즉, draw 함수 안에서 draw 함수를 호출 하는 것. 아래 코드와 같이 수정할 수 있다.

• draw 함수 안에서 draw 함수를 다시 호출 하는 부분을 유의
• h라는 높이를 받았을 때, h-1 높이로 draw 함수를 먼저 호출하고, 그 후에 h 만큼의 #을 출력.
• 여기서 내부적으로 호출된 draw 함수를 따라가다 보면 h = 0인 상황이 오게 된다.
• 따라서 그 때는 아무것도 출력을 하지 않도록 하는 조건문을 추가해줘야 한다.
• 이렇게 재귀를 사용하면 중첩 루프를 사용하지 않고도 하나의 함수로 동일한 작업을 수행할 수 있다.

※ 반복문을 쓸 수 있는데도 재귀를 사용하는 이유는 ? 루프를 중첩하게 되면 가독성이 떨어질 수 있고 변수도 더 많이 선언 해줘야 한다. 하지만 재귀를 사용하면 변수도 줄일 수 있고 가독성도 늘어나 메모리 공간도 아끼고 심미적으로 보기 괜찮다. 코드를 좀 더 간결하게 만들 수 있다.

병합 정렬

• 병합 정렬은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식
• 그리고 이 과정은 재귀적으로 구현되기 때문에 나중에 재귀를 학습하면 더 이해하기 쉽다.

----------------------------------------------------------------------------------------------------------------------
마찬가지로 다음 숫자들을 오름차순으로 정렬해 보겠습니다.

7 4 5 2 6 3 8 1

먼저 숫자들을 반으로 나눕니다.

7 4 5 2 | 6 3 8 1

그리고 나눠진 부분 중 첫번째를 한번 더 반으로 나눠봅니다.

7 4 | 5 2 | 6 3 8 1

마지막으로 한 번 더 나눠봅니다.

7 | 4 | 5 2 | 6 3 8 1

이제 숫자가 두 개 밖에 남지 않았으므로 더 이상 나누지 않고, 두 숫자를 다시 병합합니다.

단, 이 때 작은 숫자가 먼저 오도록 합니다. 4와 7의 순서를 바꿔서 병합하는 것이죠.

4 7 | 5 2 | 6 3 8 1

마찬가지로 5 2 부분도 반으로 나눈 후에 작은 숫자가 먼저 오도록 다시 병합할 수 있습니다.

4 7 | 2 5 | 6 3 8 1

그럼 이제 4 7과 2 5 두 개의 부분들을 병합하겠습니다.

각 부분들의 숫자들을 앞에서 부터 순서대로 읽어들여 비교하여 더 작은 숫자를 병합되는 부분에 가져옵니다.

즉, 4와 2를 먼저 비교해서 2를 가져옵니다. 그 후에 4와 5를 비교해서 4를 가져옵니다.

그리고 7과 5를 비교해서 5를 가져오고, 남은 7을 가져옵니다.

2 4 5 7 | 6 3 8 1

이제 남은 오른쪽 4개의 숫자들도 위와 동일한 과정을 거칩니다. 

2 4 5 7 | 1 3 6 8

마지막으로 각각 정렬된 왼쪽 4개와 오른쪽 4개의 두 부분을 병합합니다.

2와 1을 비교하고, 1을 가져옵니다. 2와 3을 비교하고, 2를 가져옵니다. 4와 3을 비교하고, 3을 가져옵니다.

4와 6을 비교하고… 이 과정을 병합이 끝날때까지 진행하면 아래와 같이 정렬이 완료됩니다.

1 2 3 4 5 6 7 8

전체 과정을 요약해서 도식화해보면 아래와 같습니다.

7 | 4 | 5 | 2 | 6 | 3 | 8 | 1 → 가장 작은 부분 (숫자 1개)으로 나눠진 결과입니다.

4   7 | 2   5 | 3   6 | 1   8 → 숫자 1개씩을 정렬하여 병합한 결과입니다.

2   4   5   7 | 1   3   6   8 → 숫자 2개씩을 정렬하여 병합한 결과입니다.

1   2   3   4   5   6   7   8 → 마지막으로 숫자 4개씩을 정렬하여 병합한 결과입니다. 

이러한 방법을 ‘병합 정렬’ 이라고 합니다.

----------------------------------------------------------------------------------------------------------------------

병합 정렬 실행 시간의 상한은 O(n log n)

숫자들을 반으로 나누는 데는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문! 

실행 시간의 하한도 역시 Ω(n log n). 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문.

※ 병합 정렬을 선택 정렬이나 버블 정렬과 비교했을 때 장점과 단점은 무엇이 있을까요? 가장큰 장점은 무엇보다 실행시간이 다른 두 정렬에 비해 빠르다는 것이고 단점이라면 이미 정렬이 되어있다면 버블정렬의 하한선이 병합정렬보다 더 빠르다는 것 즉, 더 빠르게는 할 수 없다는 얘기.

선형 검색

• 찾고자 하는 자료를 검색하는 데 사용되는 다양한 알고리즘이 있는데 그 중 하나가 선형 검색
• 선형검색은 원하는 원소가 발견될 때까지 처음부터 마지막 자료까지 차례대로 검색한다
• 이렇게 하여 선형 검색은 찾고자 하는 자료를 찾을 때까지 모든 자료를 확인해야 한다

효율성 그리고 비효율성

• 선형 검색 알고리즘은 정확하지만 아주 효율적이지 못한 방법
• 리스트의 길이가 n이라고 했을 때, 최악의 경우 리스트의 모든 원소를 확인해야 하므로 n번만큼 실행
• 여기서 최악의 상황은 찾고자 하는 자료가 맨 마지막에 있거나 리스트 안에 없는 경우
• 반대로 최선의 상황은 처음 시도했을 때 찾고자 하는 값이 있는 경우
• 평균적으로 선형 검색이 최악의 상황에서 종료되는 것에 가깝다고 가정할 수 있다.
• 선형 검색은 자료가 정렬되어 있지 않거나 그 어떤 정보도 없어 하나씩 찾아야 하는 경우에 유용
• 이러한 경우 무작위로 탐색하는 것보다 순서대로 탐색하는 것이 더 효율적

위와 같은 이유로 왜 검색 이전에 정렬해줘야 하는지 알 수 있다. 정렬은 시간이 오래 걸리고 공간을 더 차지한다.

하지만 이 추가적인 과정을 진행하면 여러 번 리스트를 검색해야 하거나 매우 큰 리스트를 검색해야 할 경우 시간을 단축할 수 있다.

주어진 배열에서 특정 값을 찾기 위해서 선형 검색을 사용한다면, 아래와 같은 코드를 작성할 수 있다.

문자열로 이루어진 배열도 비슷한 방식으로 검색할 수 있다.

만약 전화번호부에서 특정 이름을 찾아 해당하는 전화번호를 출력하는 프로그램을 작성하려면?

가장 간단한 예는 아래와 같은 프로그램이 될 것

names 배열과 numbers 배열을 따로 정의하고 names 배열에서 검색을 해서 해당하는 인덱스의 numbers 배열 값을 출력하는 것

하지만 이 경우에는 names 배열과 numbers 배열이 서로 같은 인덱스를 가져야 한다는 한계가 있다.

더 좋은 방법은 아래 코드와 같이 새로운 자료형으로 구조체를 정의해서 이름과 번호를 묶어주는 것

person 이라는 이름의 구조체를 자료형으로 정의하고 person 자료형의 배열을 선언하면 그 안에 포함된 속성값은 ‘.’으로 연결해서 접근할 수 있다. ( person a; 라는 변수가 있다면, a.name 또는 a.number 이 각각 이름과 전화번호를 저장하는 변수가 되는 것)

이렇게 함으로써 더욱 확장성 있는 전화번호부 검색 프로그램을 만들 수 있다.

버블 정렬

• 정렬되지 않은 리스트를 탐색하는 것 보다 정렬한 뒤 탐색하는 것이 더 효율적
• 정렬 알고리즘 중 하나는 버블 정렬
• 버블 정렬은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법
• 버블 정렬은 단 두 개의 요소만 정렬해주는 좁은 범위의 정렬에 집중
• 이 접근법은 간단하지만 단 하나의 요소를 정렬하기 위해 너무 많이 교환하는 낭비가 발생할 수도 있다

----------------------------------------------------------------------------------------------------------------------
아래와 같은 8개의 숫자가 임의의 순서로 나열되어 있습니다.

이 숫자들을 오름차순으로 정렬하기 위해 바로 옆의 있는 숫자들과 비교하는 방법을 사용해 보겠습니다.

6 3 8 5 2 7 4 1

먼저 가장 앞의 6과 3을 비교해서 순서를 바꿉니다.

교환 전: 6 3 8 5 2 7 4 1

교환 후: 3 6 8 5 2 7 4 1

다음 쌍인 6과 8을 비교해보면 교환할 필요가 없으므로 그대로 둡니다.

바로 다음에 있는 쌍인 8과 5를 비교해서 순서를 바꿉니다.

교환 전: 3 6 8 5 2 7 4 1

교환 후: 3 6 5 8 2 7 4 1

이런 식으로 숫자 끝까지 진행하면 아래와 같이 정렬이 됩니다.

3 6 5 2 7 4 1 8

하지만 아직 오름차순으로 정렬이 되지 않았기 때문에, 다시 처음부터 동일한 작업을 반복합니다.

3 6 5 2 7 4 1 8

3 6 5 2 7 4 1 8 (교환)

3 5 6 2 7 4 1 8 (교환)

3 5 2 6 7 4 1 8 

3 5 2 6 7 4 1 8 (교환)

3 5 2 6 4 7 1 8 (교환)

3 5 2 6 4 1 7 8

조금 더 잘 정렬이 되었습니다. 이 과정을 끝까지 반복하면 최종적으로 아래와 같이 오름차순 정렬이 될 것입니다.

1 2 4 3 5 6 7 8

이러한 정렬 방식을 ‘버블 정렬’이라고 합니다.

마치 거품이(비교 및 교환이) 터지면서 위로 올라오는 (배열의 옆으로 이동하는) 방식이기 때문입니다.

----------------------------------------------------------------------------------------------------------------------

버블 정렬의 의사코드

중첩 루프를 돌아야 하고, n개의 값이 주어졌을 때 각 루프는 각각 n-1번, n-2번 반복되므로  

(n-1)*(n-2) = n^2-3n+2(n−1)∗(n−2)=n​2​​−3n+2  번의 비교 및 교환이 필요

여기서 가장 크기가 큰 요소는 n^2 이므로 위와 같은 코드로 작성한 버블 정렬 실행 시간의 상한은 O(n^2)

정렬이 되어 있는지 여부에 관계 없이 루프를 돌며 비교를 해야 하므로 위와 같은 코드로 작성한 버블 정렬의 실행 시간의 하한도 여전히 Ω(n^2)

선택 정렬

• 배열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬
• 선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가

----------------------------------------------------------------------------------------------------------------------
다음과 같은 정렬되지 않은 숫자들을 오름차순 정렬해보도록 하겠습니다.

6 3 8 5 2 7 4 1

먼저 아래 숫자들 중에서 가장 작은 값을 찾습니다.

6 3 8 5 2 7 4 1

가장 작은 값인 1은 가장 앞에 있어야 하므로 현재 리스트의 첫 번째 값인 6과 교환합니다.

1 3 8 5 2 7 4 6

그리고 정렬되어 있는 1은 제외하고, 두 번째 숫자부터 시작해서 또 가장 작은 값을 찾습니다.

1 3 8 5 2 7 4 6

가장 작은 값인 2는 정렬되지 않는 숫자들 중에서 가장 앞에 있어야 하므로 3과 교환합니다.

1 2 8 5 3 7 4 6

이 과정을 더 이상 교환이 일어나지 않을때까지 반복하면, 아래와 같이 오름차순 정렬이 완료됩니다.

1 2 3 4 5 6 7 8

----------------------------------------------------------------------------------------------------------------------

선택정렬의 의사코드

여기서도 두 번의 루프를 돌아야 한다.

바깥 루프에서는 숫자들을 처음부터 순서대로 방문하고, 안쪽 루프에서는 가장 작은 값을 찾아야 한다.

따라서 소요 시간의 상한은 O(n^2), 하한도 마찬가지로 Ω(n^2)로 버블 정렬과 동일

배열은 한 자료형의 여러 값들이 메모리상에 모여 있는 구조. 컴퓨터는 이 값들에 접근할 때 배열의 인덱스 하나하나를 접근한다.

만약 어떤 값이 배열 안에 속해 있는지를 찾아 보기 위해서는 배열이 정렬되어 있는지 여부에 따라 아래와 같은 방법을 사용할 수 있다.

선형 검색

배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 방문하여 그 값이 속하는지를 검사.

아래 의사코드와 같이 나타낼 수 있다.

이진 검색

만약 배열이 정렬되어 있다면, 배열 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작은(작은 값이 저장되어 있는) 인덱스 또는 큰 (큰 값이 저장되어 있는) 인덱스로 이동을 반복하면 된다.

아래 의사코드와 같이 나타낼 수 있다.

알고리즘 표기법

위와 같은 그림을 공식으로 표기한 것이 Big O 표기법 이다.

여기서 O는 “on the order of”의 약자로, 쉽게 생각하면 “~만큼의 정도로 커지는” 것이라고 볼 수 있다.

O(n) 은 n만큼 커지는 것이므로 n이 늘어날수록 선형적으로 증가하고, O(n/2)도 결국 n이 매우 커지면 1/2은 큰 의미가 없어지므로 O(n)이라고 볼 수 있다.

주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용된다.

• O(n^2)
• O(n log n)
• O(n) - 선형 검색
• O(log n) - 이진 검색
• O(1)

Big O가 알고리즘 실행 시간의 상한을 나타낸 것이라면, 반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타낸다.

예를 들어 선형 검색에서는 n개의 항목이 있을때 최대 n번의 검색을 해야 하므로 상한이 O(n)이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 Ω(1)이 된다.

역시 아래 목록과 같은 Big Ω 표기가 많이 사용된다.

• Ω(n^2)
• Ω(n log n)
• Ω(n) - 배열 안에 존재하는 값의 개수 세기
• Ω(log n)
• Ω(1) - 선형 검색, 이진 검색

※ 실행시간의 상한이 낮은 알고리즘이 더 좋을까, 하한이 낮은 알고리즘이 더 좋을까?

하한선이 낮은경우는 특정상황에 의존하여 결과가 나오길 기대해야 하지만 상한선이 낮은경우는 평균적으로 실행시간이 줄어드는것을 의미하기 때문에 실행시간의 상한선이 낮은 알고리즘이 더 좋다. 최대치를 알고 코드를 작성하는것이 효율적으로 코드를 작성할 수 있다고 생각

문자열과 배열

• 문자열(string) 자료형의 데이터 = 사실 문자(char) 자료형의 데이터들의 배열
• string s = “HI!”; 과 같이 문자열 s가 정의되어 있다고 생각해보면,
• s는 문자의 배열이기 때문에 메모리상에 아래 그림과 같이 저장되고, 인덱스로 각 문자에 접근할 수 있다.

• 가장 끝의 ‘\0’ = 문자열의 끝을 나타내는 널 종단 문자
• 단순히 모든 비트가 0인 1바이트를 의미함

※ 아래 코드와 같이 여러 문자열이 동시에 선언된 경우

• names라는 문자열 형식의 배열에 네 개의 이름이 저장되어있다.
• 첫 번째 printf에서는 names의 첫번째 인덱스의 값, 즉 “EMMA”를 출력
• 두 번째 printf에서는 형식 지정자가 %s가 아닌 %c로 설정되어 있음
• 따라서 출력하는 것은 문자열이 아닌 문자
• 여기서는 각 이름의 두번째 문자를 출력하고자 한다.
• 이는 names[0][1]과 같이 2차원 배열을 통해 접근할 수 있다.
• 다시 말해 names[0][1]는 names의 첫 번째 값, 즉 “EMMA”라는 문자열에서, 그 두번째 값, 즉 ‘M’ 이라는 문자를 의미

아래 그림에서 names가 실제 메모리상에 저장된 예시와 해당하는 인덱스를 확인할 수 있다.

문자열의 활용

① 문자열의 길이 및 탐색

• 사용자로 부터 문자열을 입력받아 한 글자씩 출력하는 프로그램 만들기
• 간단하게 for 루프를 통해 문자열의 인덱스를 하나씩 증가시켜가면서 해당하는 문자를 출력하면 되는데,
• 문자열의 끝을 알 수 있는 방법은 ? 해당하는 인덱스의 문자가 널 종단 문자, 즉 ‘\0’와 일치하는지 검사하는 것
• 즉, s라는 문자열이 있다고 할 때 for (int i = 0; s[i] != ‘\0’; i++) { ..} 과 같은 루프를 사용하면 된다.
• 하지만 아래 코드와 같이 strlen() 이라는 함수를 사용할 수도 있다.

• strlen = 문자열의 길이를 알려주는 함수, string.h 라이브러리 안에 포함되어 있음
• 위 코드에서는 n이라는 변수에 문자열 s의 길이를 저장하고, 해당 길이 만큼만 for 루프를 순환
• → 일일이 널 종단 문자를 검사하는 것 보다 훨씬 효율적!

② 문자열 탐색 및 수정

< 사용자로부터 문자열을 입력받아 대문자로 바꿔주는 프로그램 >

• 먼저 사용자로부터 입력받은 문자를 s라는 변수에 저장
• 그리고 s의 길이만큼 for 루프를 돌면서, 각 인덱스에 해당하는 문자가 ‘a’보다 크고 ‘z’보다 작은지 검사
• 즉, 소문자인지 검사하는 것과 동일
• 여기서 문자의 대소비교가 가능한 이유는 ASCII값, 즉 그 문자가 정의되는 ASCII 코드 상에서의 숫자값으로 비교할 수 있기 때문
• 또한 알파벳의 ASCII 값을 잘 살펴보면 각 알파벳의 소문자와 대문자는 32씩 차이가 남을 확인할 수 있다.
• 따라서 각 문자가 소문자인 경우 그 값에서 32를 뺀 후에 ‘문자’ 형태로 출력하면 대문자가 출력이 된다.
• 각 문자가 이미 대문자인 경우는 그냥 그대로 출력

※ 이와 동일한 작업을 수행하는 함수가 ctype 라이브러리에 toupper() 이라는 함수로 정의되어 있다. (아래 코드 참조)

명령행 인자

• main도 그 형태를 보면 하나의 함수 ! 
• main() 안에 기계적으로 void 라고 입력하는 대신 아래 코드와 같이 argc, argv 를 정의해 보면,

• 첫번째 변수 argc는 main 함수가 받게 될 입력의 개수
• 그리고 argv[]는 그 입력이 포함되어 있는 배열
• 프로그램을 명령행에서 실행하므로, 입력은 문자열로 주어진다. 따라서 argv[]는 string 배열이 됨
• argv[0]는 기본적으로 프로그램의 이름으로 저장됨
• 만약 하나의 입력이 더 주어진다면 argv[1]에 저장될 것
• 예를 들어 위 프로그램을 “arg.c”라는 이름으로 저장하고 컴파일 한 후 “./argc”로 실행해보면 “hello, world”라는 값이 출력됨
• 명령행 인자에 주어진 값이 프로그램 이름 하나밖에 없기 때문
• 하지만 “./argc David”로 실행해보면 “hello, David”라는 값이 출력됩니다.
• 명령행 인자에 David라는 값이 추가로 입력되었고, 따라서 argc 는 2, argv[1] 은 “David”가 되기 때문